EPIC FAIL: SISTEMA y CONVERSION DE UNIDADES y VECTORES: Física

SISTEMA DE UNIDADES

Un sistema de unidades es un conjunto consistente de unidades de medida. Definen un conjunto básico de unidades de medida a partir del cual se derivan el resto. Existen varios sistemas de unidades:

Sistema Internacional de Unidades o SI: es el sistema más usado. Sus unidades básicas son: el metro, el kilogramo, el segundo, el ampere, el kelvin, la candela y el mol. Las demás unidades son derivadas del Sistema Internacional.
Sistema métrico decimal: primer sistema unificado de medidas.
Sistema cegesimal o CGS: denominado así porque sus unidades básicas son el centímetro, el gramo y el segundo.
Sistema Natural: en el cual las unidades se escogen de forma que ciertas constantes físicas valgan exactamente 1.
Sistema técnico de unidades: derivado del sistema métrico con unidades del anterior. Este sistema está en desuso.
Sistema anglosajón de unidades: aún utilizado en algunos países anglosajones. Muchos de ellos lo están reemplazando por el Sistema Internacional de Unidades.

CONVERSION DE UNIDADES

La conversión de unidades es la transformación de una unidad en otra.

Este proceso se realiza con el uso de los factores de conversión y las muy útiles tablas de conversión.

Bastaría multiplicar por una fracción (factor de conversión) y el resultado es otra medida equivalente, en la que han cambiado las unidades.

Cuando el cambio de unidades implica la transformación de varias unidades se pueden utilizar varios factores de conversión uno tras otro, de forma que el resultado final será la medida equivalente en las unidades que buscamos, por ejemplo si queremos pasar 8 metros a yardas, lo único que tenemos que hacer es multiplicar 8 x (0.914)=7.312 yardas.

VECTORES

En física, un vector es una herramienta geométrica utilizada para representar una magnitud física del cual depende únicamente un módulo (o longitud) y una dirección (u orientación) para quedar definido.

Notación

Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flecha sobre la letra que designa su módulo (el cual es un escalar).

Suma de vectores

Para sumar dos vectores libres (vector y vector) se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Método del paralelogramo

Este método permite solamente sumar vectores de a pares. Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, trazando rectas paralelas a cada uno de los vectores, en el extremo del otro y de igual longitud, formando así un paralelogramo (ver gráfico a la derecha). El resultado de la suma es la diagonal de dicho paralelogramo que parte del origen común de ambos vectores.

Método del triángulo

Consiste en disponer gráficamente un vector a continuación de otro; es decir, el origen de cada uno de los vectores se lleva sobre el extremo del otro. El vector resultante es aquél que nace en el origen del primer vector y termina en el extremo del último.

Método analítico para la suma y diferencia de vectores

Dados dos vectores libres,

$\mathbf{a} = (a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k})$

$\mathbf{b} = (b_x \mathbf{i} + b_y \mathbf{j} + b_z \mathbf{k})$

El resultado de su suma o de su diferencia se expresa en la forma

$\mathbf{a} \pm \mathbf{b} = (a_x \mathbf{i} +a_y \mathbf{j} +a_z \mathbf{k}) \pm (b_x \mathbf{i} +b_y \mathbf{j} +b_z \mathbf{k})$

y ordenando las componentes,

$\mathbf{a} \pm \mathbf{b} = (a_x \pm b_x) \mathbf{i} + (a_y \pm b_y) \mathbf{j} + (a_z \pm b_z)\mathbf{k}$

Con la notación matricial sería

$\mathbf{a} \pm \mathbf{b} = \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} \pm \begin{bmatrix} b_x\\ b_y\\ b_z\\\end{bmatrix} = \begin{bmatrix} a_x\pm b_x\\ a_y\pm b_y\\ a_z\pm bz\\\end{bmatrix}$

Conocidos los módulos de dos vectores dados, $\mathbf{a}$ y $\mathbf{b}$ , así como el ángulo

θ

que forman entre sí, el módulo de $\mathbf{a} \pm \mathbf{b}$ es:

$|\mathbf{a} \pm \mathbf{b}| = \sqrt{a^2 + b^2 - 2ab \cos \theta}$

La deducción de esta expresión puede consultarse en deducción del módulo de la suma.

Producto de un vector por un escalar

El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es igual a la del vector, o contraria a este si el escalar es negativo.

Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como indica el escalar.

Sean $p \,$ un escalar y $\mathbf{a}$ un vector, el producto de $p \,$ por $\mathbf{a}$ se representa $p \, \mathbf{a}$ y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es,

$p \, \mathbf{a} = pa_x \mathbf{i} + pa_y \mathbf{j} + pa_z \mathbf{k}$

Con la notación matricial sería

$p \, \mathbf{a} = p \, \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} = \begin{bmatrix} p\,a_x\\ p\,a_y\\ p\,a_z\\\end{bmatrix}$

Producto Escalar

El producto escalar es una operación definida sobre dos vectores de un espacio euclídeo cuyo resultado es un número o escalar.

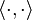Un producto escalar se puede expresar como una aplicación $\langle \cdot,\cdot \rangle: V \times V \longrightarrow \mathbb{K}$ donde V es un espacio vectorial y $\mathbb{K}$ es el cuerpo sobre el que está definido V. $\langle \cdot,\cdot \rangle$ debe satisfacer las siguientes condiciones:

Linealidad por la izquierda y por la derecha: $\langle ax+by,z \rangle = a \langle x,z \rangle + b \langle y,z \rangle$ , y análogamente $\langle x, ay+bz \rangle = a \langle x, y \rangle + b \langle x,z \rangle$
Hermiticidad: $\langle x,y \rangle = \overline{\langle y,x \rangle}$ ,
Definida positiva: $\langle x,x \rangle \geq 0 \,$ , y $\langle x,x \rangle = 0 \,$ si y sólo si x = 0,

donde $x, y, z \in V$ son vectores de V, $a, b \in \mathbb{K}$ representan escalares del cuerpo $\mathbb{K}$ y $\overline{c}$ es el conjugado del complejo c.

Si el cuerpo tiene parte imaginaria nula (v.g., $\mathbb{R}$ ), la propiedad de ser sesquilineal se convierte en ser bilineal y el ser hermítica se convierte en ser simétrica.

También suele representarse por $(\cdot|\cdot)$ o por $\bullet$ .

Un espacio vectorial sobre el cuerpo $\mathbb{R}$ o $\mathbb{C}$ dotado de un producto escalar se denomina espacio prehilbert o espacio prehilbertiano. Si además es completo, se dice que es un espacio de hilbert, y si la dimensión es finita, se dirá que es un espacio euclídeo.

Todo producto escalar induce una norma sobre el espacio en el que está definido, de la siguiente manera:

$\|x\|:= \sqrt{\langle x,x \rangle}$ .

El producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo tridimensional que da como resultado un vector ortogonal a los dos vectores originales.

Sean dos vectores $\mathbf a$ y $\mathbf b$ en el espacio vectorial $\mathbb{R}^3$ . El producto vectorial entre $\mathbf a\,$ y $\mathbf b\,$ da como resultado un nuevo vector, $\mathbf c\,$ . Para definir este nuevo vector es necesario especificar su módulo y dirección:

El módulo de $\mathbf c\,$ está dado por

$c = a \, b \, \sin\theta$

donde θ es el ángulo determinado por los vectores a y b.

La dirección del vector c, que es ortogonal a a y ortogonal a b, está dada por la regla de la mano derecha.

El producto vectorial entre a y b se denota mediante a × b, por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto vectorial mediante a ∧ b.

El producto vectorial puede definirse de una manera más compacta de la siguiente manera:

${\mathbf a \times \mathbf b = {a} \, {b} \, {\sin}{\theta} \ \hat\mathbf n}$

donde $\hat\mathbf n$ es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorcho.

Derivada de un vector

Dado un vector que es función de una variable independiente

$\mathbf{a}(t)= a_x(t) \mathbf{i} +a_y(t) \mathbf{j} +a_z(t) \mathbf{k}$

Calculamos la derivada del vector con respecto de la variable t, calculando la derivada de cada una de sus componentes como si de escalares se tratara:

$\frac{d}{dt}\mathbf{a}(t)= \frac{d}{dt}a_x(t) \mathbf{i} + \frac{d}{dt}a_y(t) \mathbf{j} + \frac{d}{dt}a_z(t) \mathbf{k}$

teniendo en cuenta que los vectores unitarios son constantes en módulo y dirección.

Con notación matricial sería

$\frac{d}{dt}\mathbf{a}(t)= \frac{d}{dt} \, \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} = \begin{bmatrix} \frac{d}{dt}a_x\\ \frac{d}{dt}a_y\\ \frac{d}{dt}a_z\\\end{bmatrix}$

$\mathbf{r}(t)=\sin(t) \mathbf{i}+\cos(t)\mathbf{j}+ 5t\mathbf{k}$

Veamos un ejemplo de derivación de un vector, partiendo de una función vectorial:

$\mathbf{r}(t) = \sin(t) \mathbf{i} + \cos(t) \mathbf{j} + 5t \mathbf{k}$

Esta función representa una curva helicoidal alrededor del eje z, de radio unidad, como se ilustra en la figura. Podemos imaginar que esta curva es la trayectoria de una partícula y la función $\mathbf r (t)\,$ representa el vector posición en función del tiempo t. Derivando tendremos:

$\frac{d\mathbf{r}(t)}{dt} = \frac{d}{dt}\sin(t) \mathbf{i} + \frac{d}{dt}\cos(t) \mathbf{j} + \frac{d}{dt}5t \mathbf{k}$

Realizando la derivada:

$\frac{d\mathbf{r}(t)}{dt} = \cos(t) \mathbf{i} - \sin (t) \mathbf{j} + 5 \mathbf{k}$

La derivada del vector posición respecto al tiempo es la velocidad, así que esta segunda función determina el vector velocidad de la partícula en función del tiempo, podemos escribir:

$\mathbf{v}(t) = \cos(t) \mathbf{i} - \sin(t) \mathbf{j} + 5 \mathbf{k}$

Este vector velocidad es un vector tangente a la trayectoria en el punto ocupado por la partícula en cada instante. Si derivásemos de nuevo obtendríamos el vector aceleración.

Ángulo entre dos vectores

El ángulo determinado por las direcciones de dos vectores $\mathbf{a}$ y $\mathbf{b}$ viene dado por:

$\cos \theta = \frac {\mathbf a \cdot \mathbf b}{|\mathbf{a}| \, |\mathbf{b}|}$

Cambio de base vectorial

Las rotaciones son transformaciones lineales que conservan las normas en espacios vectoriales en los que se ha definido una operación de producto interior. La matriz de transformación tiene la propiedad de ser una matriz unitaria, es decir, es ortogonal y su determinante es 1. Sea un vector $\scriptstyle \mathbf A$ expresado en una sistema de coordenadas cartesianas (x, y, z) con una base vectorial $\mathcal{B}$ asociada definida por los versores $\left( \mathbf i, \mathbf j,\mathbf k\, \right)$ ; esto es,

$\mathbf A=\begin{bmatrix} A_x \\ A_y \\ A_z \end{bmatrix}_{\mathcal{B}}$

Ahora, supongamos que giramos el sistema de ejes coordenados, manteniendo fijo el origen del mismo, de modo que obtengamos un nuevo triedro ortogonal de ejes (x′, y′, z′), con una base vectorial $\mathcal{B}'$ asociada definida por los versores $\left( \mathbf i', \mathbf j',\mathbf k'\, \right)$ . Las componentes del vector $\mathbf A \,$ en esta nueva base vectorial serán:

$\mathbf A=\begin{bmatrix} A'_x \\ A'_y \\ A'_z \end{bmatrix}_{\mathcal{B}'}$

La operación de rotación de la base vectorial siempre puede expresarse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector):

$\mathbb R \, \mathbf A_{\mathcal{B}} = \mathbf A_{\mathcal{B}'}$

que es la matriz de transformación para el cambio de base vectorial.

EPIC FAIL

6 de marzo de 2011

SISTEMA y CONVERSION DE UNIDADES y VECTORES: Física